Robust RL Guidance for Far-Range Rendezvous

Overview

This work addresses far-range rendezvous under angles-only navigation by combining nominal trajectory planning under fuel, safety, and observability constraints with a reinforcement-learning guidance layer trained under realistic uncertainties. The goal of the RL guidance is to maintain safety and observability while minimizing fuel consumption during execution.

Problem

Angles-only navigation can be weakly observable unless the relative geometry is actively shaped. Far-range rendezvous must maintain passive and active safety throughout. Existing guidance strategies are seldom focused on fuel conservation.

Approach

Two-stage pipeline: (1) nominal plan optimised for Δv/observability/safety; (2) RL selects a contraction parameter used by a convex optimisation step to compute guidance impulses.

Result

Demonstrated Δv savings relative to alternative guidance strategies in the presented scenario while maintaining safety and observability.

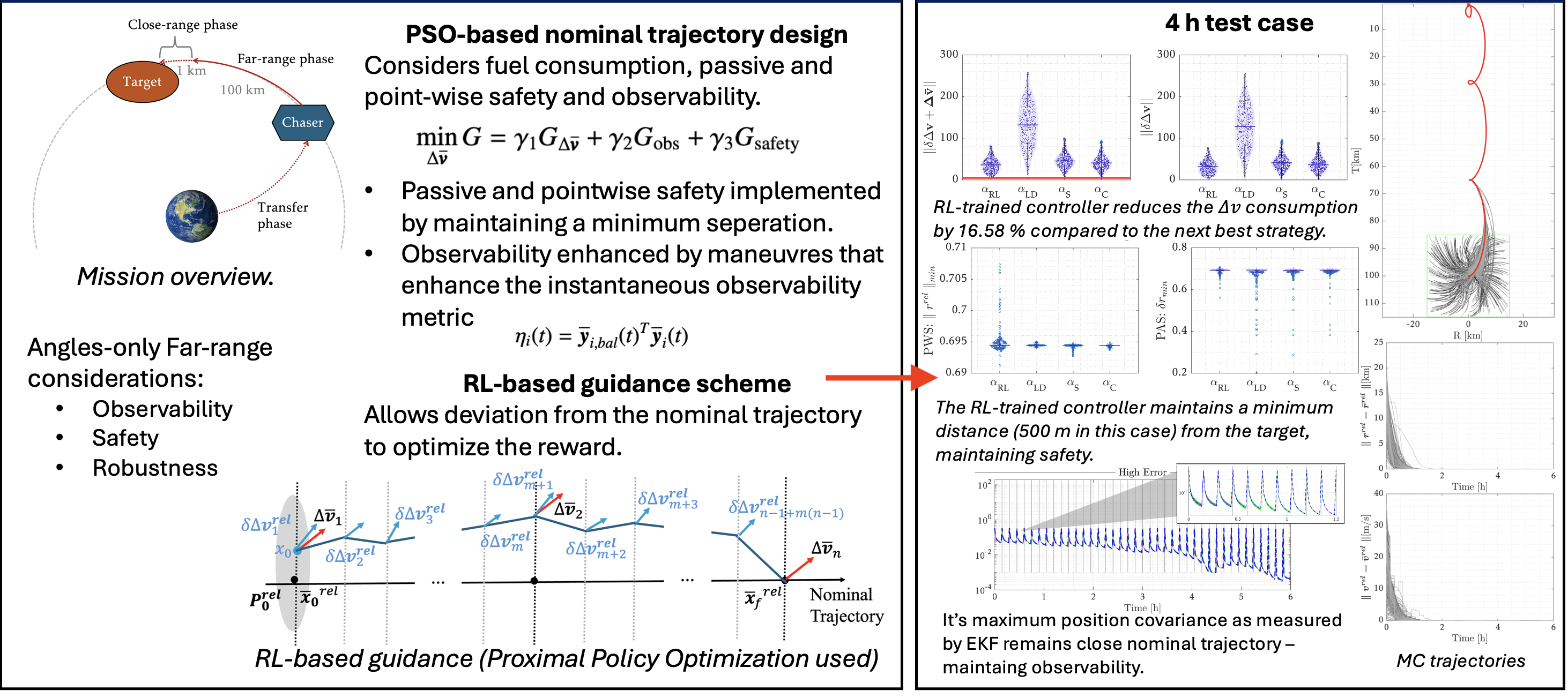
Motivation

Far-range rendezvous demands robust execution in the presence of initial state dispersion and actuation errors. With angles-only measurements, observability—particularly range—can degrade unless the guidance policy actively manages relative motion geometry. At the same time, safety constraints (e.g., keep-out regions and passive safety) must be respected throughout the approach.

Method

The approach is a two-stage pipeline: nominal impulsive trajectory design that explicitly trades fuel, observability, and safety, followed by an RL-guided execution layer that selects a contraction level and solves a small convex problem to compute guidance impulses online.

Stage 1 — Nominal trajectory planning

We select a sequence of impulsive manoeuvres \(\{\Delta {\mathbf{v}}_i\}_{i=1}^{n}\) by minimising a composite objective:

Optimisation objective \[ \min_{\{\Delta {\mathbf{v}}_i\}} \; G \;=\; G_{\Delta {v}} \;+\; G_{\mathrm{obs}} \;+\; G_{\mathrm{safe}}. \]

Fuel / \(\Delta v\) metric

Total impulse magnitude over the plan:

G_{\Delta {v}}=\sum_{i=1}^{n}\left\lVert \Delta {\mathbf{v}}_i \right\rVert_2.

The final impulse is computed via the Lambert's method to ensure the terminal target state is reached.

Observability metric

Observability is encouraged by shaping the measurement profile. The score used is the alignment between ballistic and forced measurement directions:

\eta(t_k)={\mathbf{y}}_{\mathrm{bal}}(t_k)^{\top}\,{\mathbf{y}}(t_k), \] \[ G_{\mathrm{obs}}=\sum_{k=0}^{t_f}\eta(t_k).

Blue: \({\mathbf{y}}(t)\). Black: \({\mathbf{y}}_{\mathrm{bal}}(t)\).

Safety metric

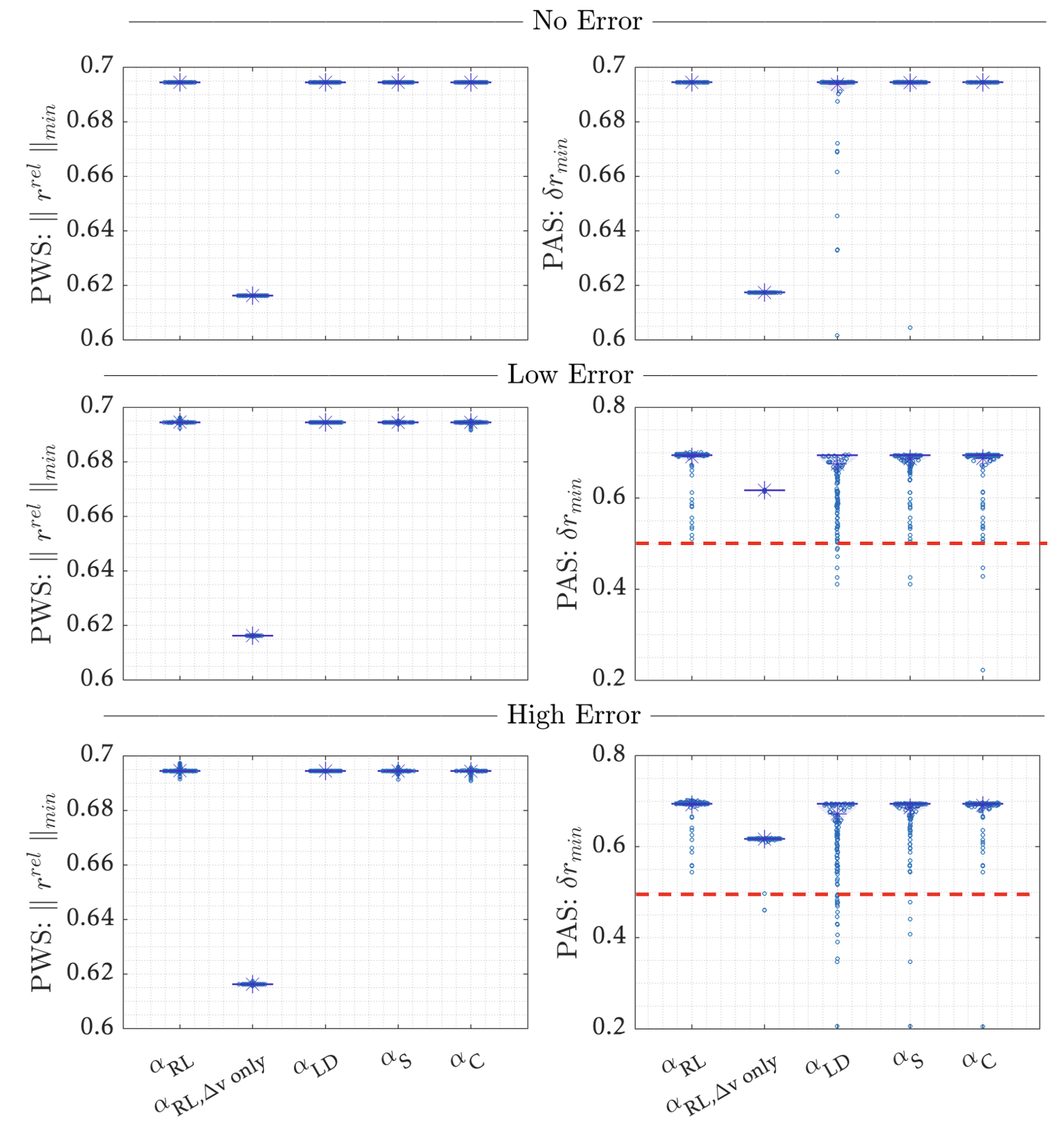
Point-wise safety (PWS) and passive safety (PAS) are encoded via penalties:

\[ G_{\mathrm{safe}}=\sum_{k=0}^{t_f}\Big(\zeta_{\mathrm{PAS}}(t_k)+\zeta_{\mathrm{PWS}}(t_k)\Big). \] where \[ \zeta_{\mathrm{PWS}}(t)=\exp\!\left(-\frac{\|\mathbf{r}^{\mathrm{rel}}(t)\|_2^2}{2\sigma^2}\right). \] \[ \zeta_{\mathrm{PAS}}(t)=\exp\!\left(-\frac{\mathbf{\delta r}^{min}_{PAS}(t)^2}{2\sigma^2}\right). \] where \(\mathbf{r}^{\mathrm{rel}}(t)\) is the relative position (so \(\|\mathbf{r}^{\mathrm{rel}}(t)\|_2\) is the relative distance), and \(\delta r_{\mathrm{PAS}}^{\min}(t)\) is the minimum passive separation distance.

Stage 2 — RL guidance + convex optimisation

At each guidance update \(k\), a PPO policy outputs a contraction parameter \(\alpha_k\) that limits how quickly the deviation from the nominal plan must shrink. Given \(\alpha_k\), we compute the minimum-effort impulse by solving a small convex programme.

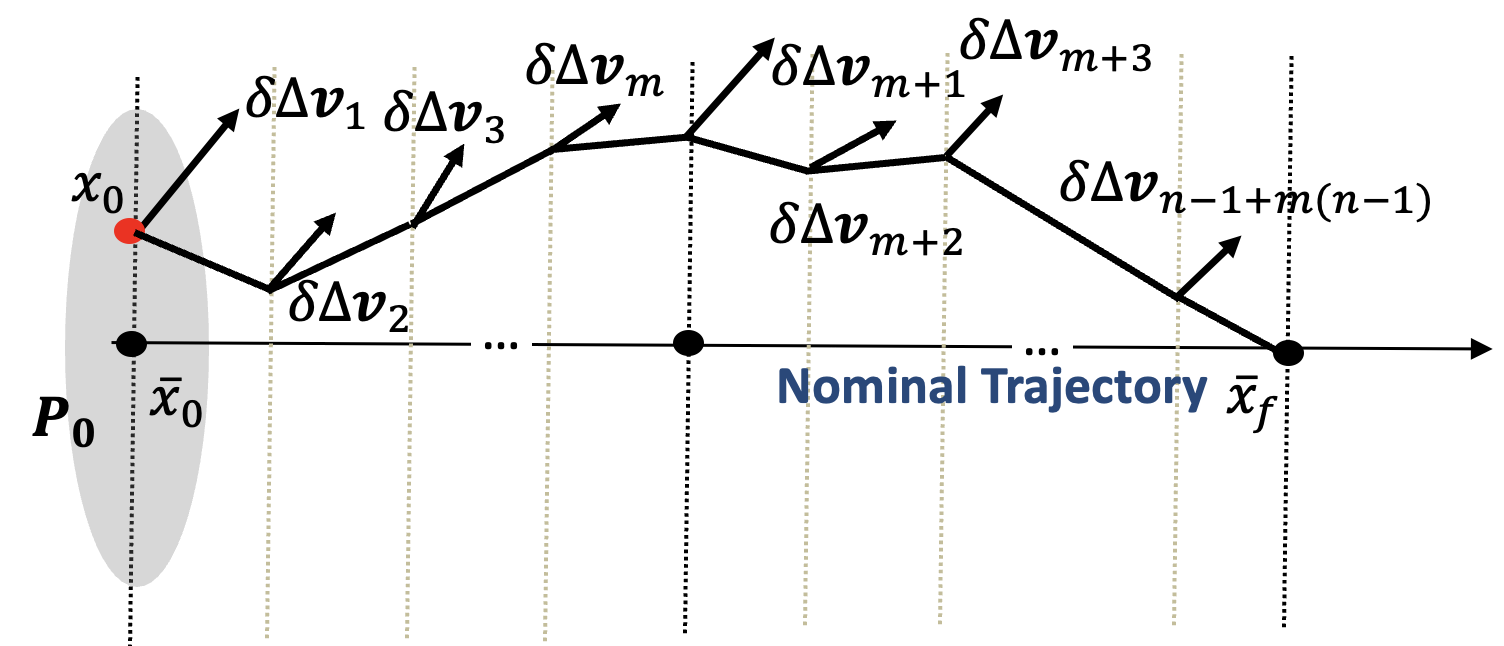
Nominal trajectory and corrective impulses illustration — Nominal trajectory and corrective impulses \(\delta\Delta \mathbf{v}\) applied during execution.

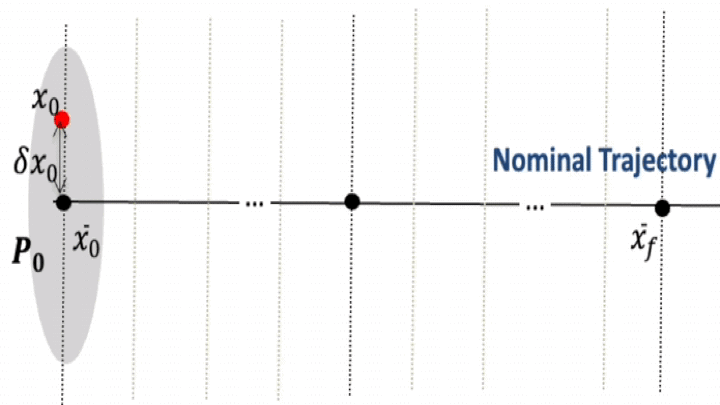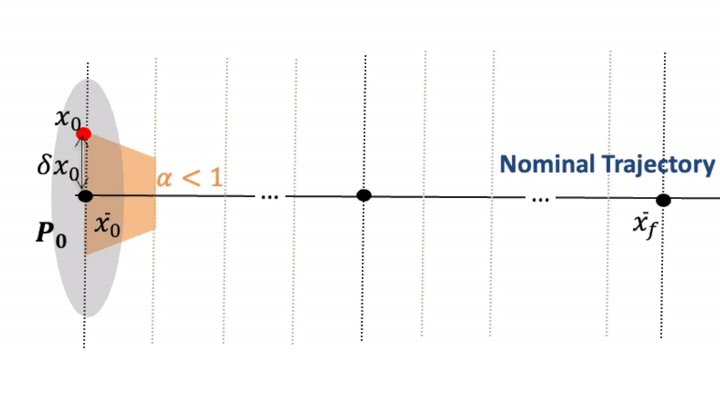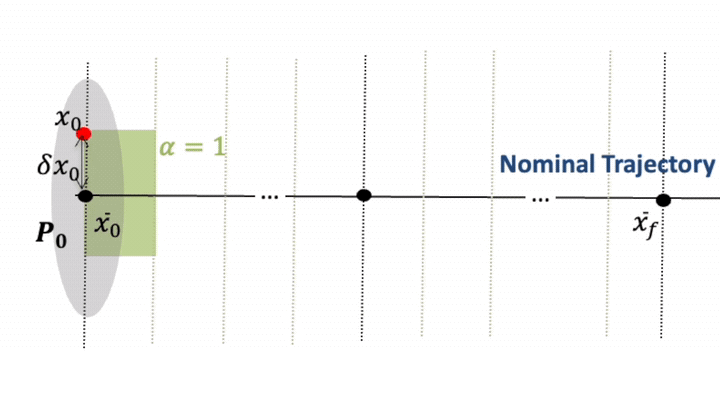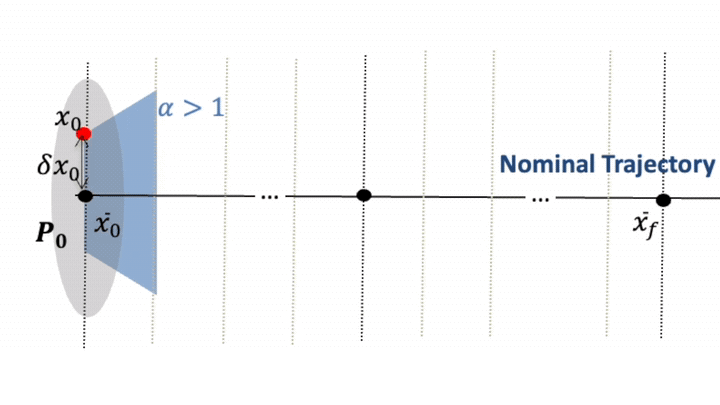
Animation: RL-selected contraction parameter alpha — RL selects the contraction parameter \(\alpha\), shaping the online guidance update.

QCQP problem \[ \begin{aligned} \min_{\Delta {\mathbf{v}}_k}\quad & \left\lVert \Delta {\mathbf{v}}_k \right\rVert_2 \\ \text{s.t.}\quad & \mathbf{x}_{k+1} = \mathbf{A}\mathbf{x}_k + \mathbf{B}\Delta {\mathbf{v}}_k, \\ & \left\lVert \mathbf{x}_{k+1}-\mathbf{x}^{\mathrm{nom}}_{k+1} \right\rVert_2 \le \alpha_k \left\lVert \mathbf{x}_k-\mathbf{x}^{\mathrm{nom}}_k \right\rVert_2 \end{aligned} \]

Training is performed in a stochastic environment (initial state errors, thrust errors), with a reward that discourages \(\Delta v\), constraint violations, and poor observability, while encouraging convergence to the terminal set.

Reward \[ R_j \;=\; -\Big(\|\Delta \mathbf{v}_j\|_2 \;+\; P_{j,\mathrm{obs}} \;+\; P_{j,\mathrm{safe}}\Big). \]

Results

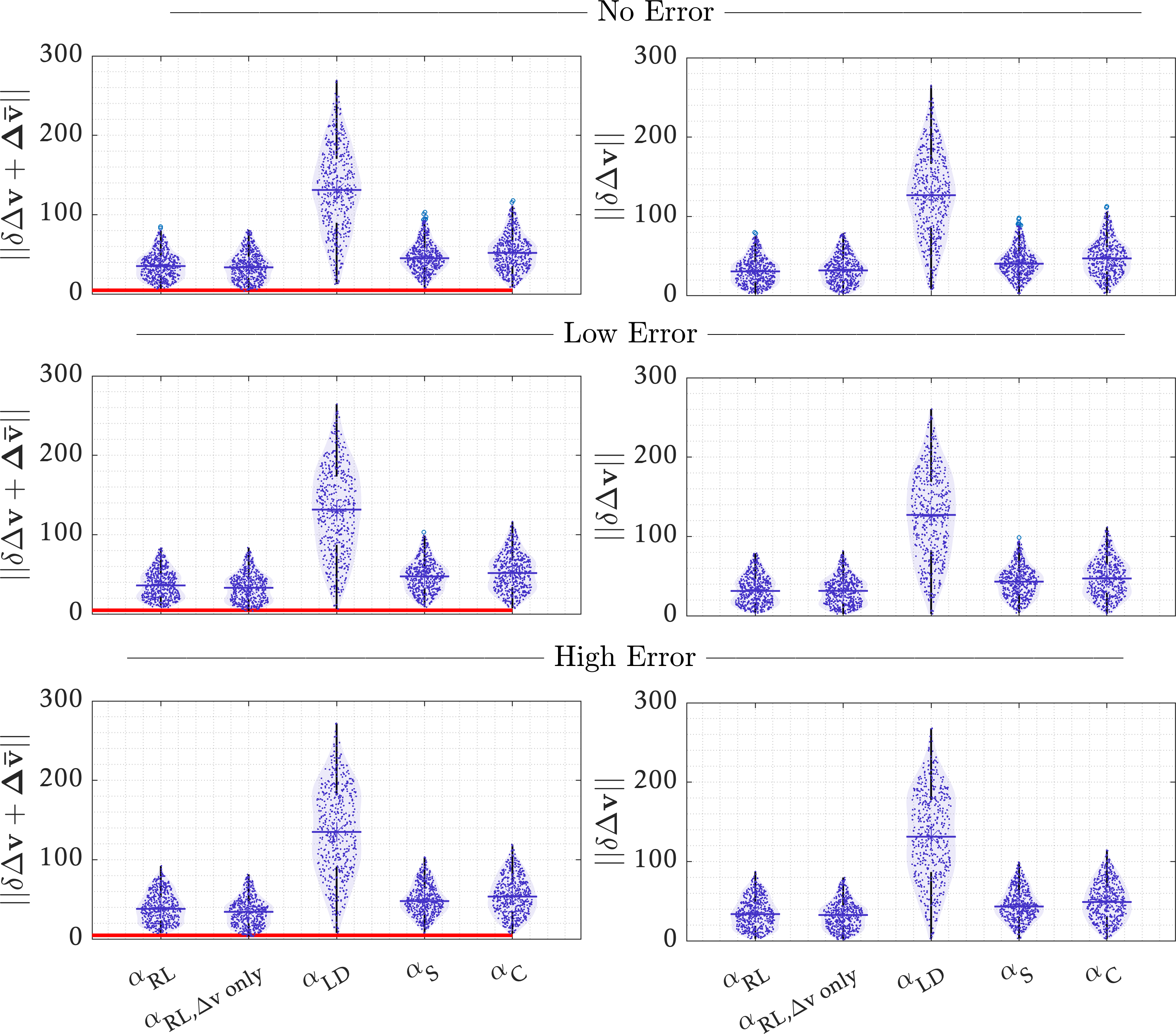
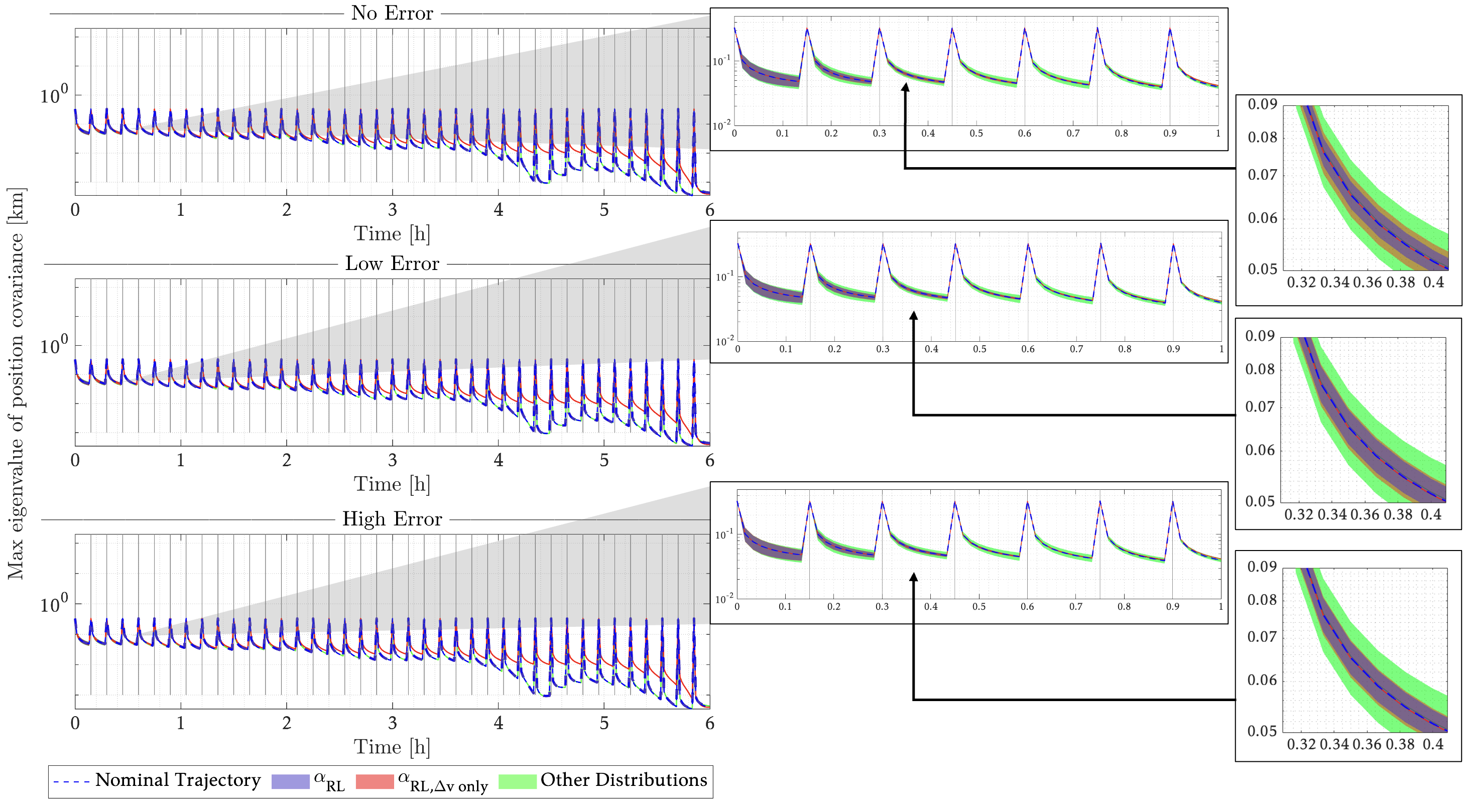
Performance is evaluated using 500-sample Monte Carlo simulations under three thrust-error regimes (no / low / high). We report total \(\Delta v\) consumption, safety with a 500 m keep-out zone (KOZ), and observability using the EKF maximum position-covariance eigenvalue metric.

Evaluation setup

We benchmark the RL-trained contraction parameter \(\alpha_{RL}\) against fixed and heuristic contraction schedules, and evaluate robustness under zero-mean thrust errors applied to each commanded impulse. Reported “error levels” are standard deviations (bias \(=0\)).

Contraction-parameter baselines

\(\alpha_{RL}\) is learned (PPO). Baselines below are compared against it.

Method	Definition	Notes
\(\alpha_{RL}\)	\(\alpha\) from PPO policy	Learned online contraction level
\(\alpha_{LD}\)	\[ \alpha_{LD,j}=1-\frac{t_j-t_0}{t_f-t_0} \]	Linearly decreasing schedule
\(\alpha_C\)	\(\alpha_C = 0\)	Constant contraction
\(\alpha_S\)	\[ \alpha_S=\arg\min_{\alpha}\left(\sum_{k=1}^{12}\sum_{j=1}^{j_{\mathrm{end}}} R_j\right) \]	Sigma-point optimised \(\alpha\)

Thrust error levels (standard deviations)

\(\delta_{\Delta v}\) is the percent magnitude perturbation, \(\delta\beta\) is the in-plane angle perturbation (deg), and \(\delta\gamma\) is the out-of-plane angle perturbation (deg).

Simulation	\(\sigma_{\Delta v}\) (%)	\(\sigma_{\beta}\) (deg)	\(\sigma_{\gamma}\) (deg)
No error	0	0	0
Low error	2	1	1
High error	4	2	2

\[ \delta_{\Delta v,j}\sim\mathcal N(0,\sigma_{\Delta v}),\qquad \delta_{\beta,j}\sim\mathcal N(0,\sigma_{\beta}),\qquad \delta_{\gamma,j}\sim\mathcal N(0,\sigma_{\gamma}), \] \[ \Delta \mathbf v_j^{\,\mathrm{exec}} \;=\; \big(1 + \delta_{\Delta v,j}\big)\; \mathbf R\!\big(\delta_{\beta,j},\delta_{\gamma,j}\big)\; \Delta \mathbf v_j^{\,\mathrm{cmd}}. \]

Delta-v distribution across contraction strategies and error levels — \(\Delta v\) distributions across contraction strategies under no/low/high thrust error. \(\alpha_{RL}\) achieves the lowest mean \(\Delta v\) among the safe strategies.

Safety metrics for PWS and PAS under error levels — Safety evaluation: PWS minimum separation and PAS missed-impulse minimum separation. The dashed line indicates the 500 m KOZ threshold; only \(\alpha_{RL}\) maintains PAS safety across all error levels.

More figures (observability and terminal error)

EKF max eigenvalue of position covariance over time — Observability: maximum eigenvalue of EKF position covariance over time (no/low/high error). \(\alpha_{RL}\) stays close to the nominal trajectory envelope and reconverges after early deviations.

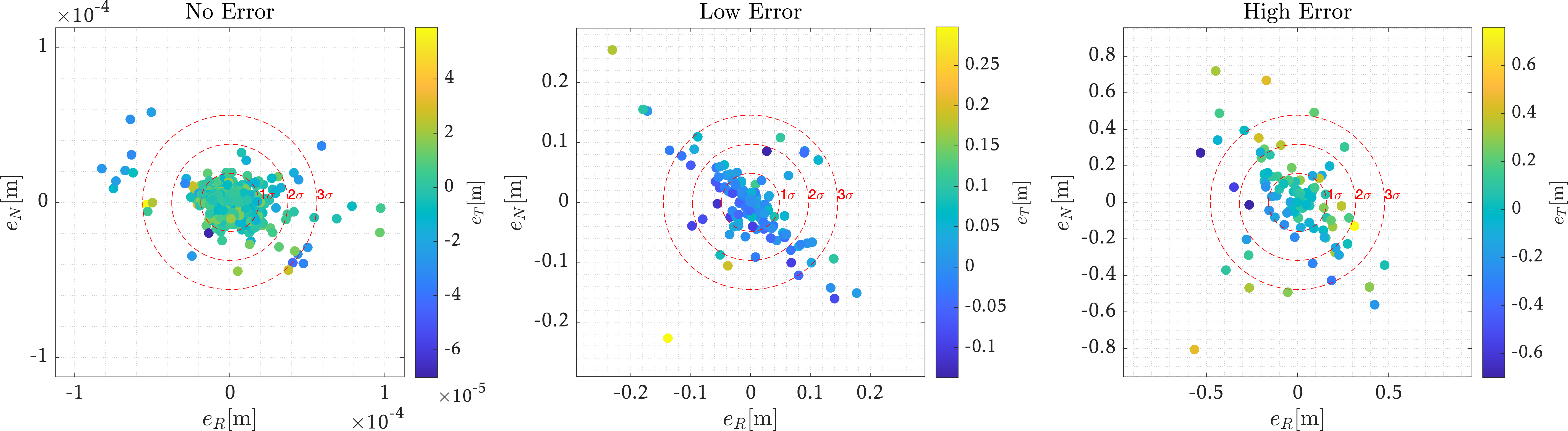
Terminal error distribution under thrust error levels — Terminal error distribution for the rendezvous terminal state under no/low/high thrust error.

Fuel savings

RL guidance achieves the lowest total \(\Delta v\) among the strategies that maintain safety and observability.

Mean total \(\Delta v\) (RL):

No error: \(37.07 \pm 17.41\) m/s
Low error: \(37.52 \pm 18.15\) m/s
High error: \(39.90 \pm 19.04\) m/s

Safety

Safety is evaluated via point-wise safety (PWS) and passive safety (PAS), with a 500 m KOZ.

\(\alpha_{RL}\) maintains KOZ compliance across all error regimes in the Monte Carlo runs.
Under PAS (missed-impulse) evaluation, only \(\alpha_{RL}\) avoids KOZ breaches across all error cases.

Observability

Observability is assessed using an EKF and the time evolution of the maximum eigenvalue of the position covariance.

\(\alpha_{RL}\) trajectories keep covariance close to the nominal profile and converge back within \(\sim\)2 h.
Non-RL baselines show broader covariance variation, often worse than the nominal trajectory.

BibTeX

Citation

@article{WIJAYATUNGA2025109996,
title = {Robust trajectory design and guidance for far-range rendezvous using reinforcement learning with safety and observability considerations},
journal = {Aerospace Science and Technology},
volume = {159},
pages = {109996},
year = {2025},
issn = {1270-9638},
doi = {https://doi.org/10.1016/j.ast.2025.109996},
author = {Minduli Charithma Wijayatunga and Roberto Armellin and Harry Holt}}